NRTL模型
于1968年,Renon和Prausnitz(AIChE J. 1968, 14(1): 135)根據(jù)局部組成概念提出了NRTL(Non-Random Two Liquids,非隨機(jī)兩流體)方程,在關(guān)聯(lián)局部組成與總體組成的Boltzmann型方程中引入了一個(gè)能反映體系特征的非隨機(jī)參數(shù)α12。但與Wilson方程不同的是,NRTL方程可同時(shí)適用于部分互溶及完全互溶系統(tǒng)。
NRTL方程的溶液超額自由焓表達(dá)式為:
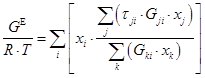 (1)
(1)
由此得到的活度系數(shù)方程為:
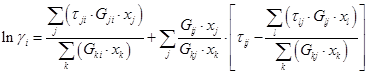 (2)
(2)
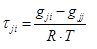 (3)
(3)
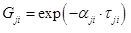 (4)
(4)
其中gji的含義與Wilson方程中λji相似,表示i–j兩種不同分子間相互作用的能量參數(shù);參數(shù)αji與混合物中的非隨機(jī)性有關(guān),當(dāng)αji為零時(shí),混合物完全隨機(jī)。對(duì)于二元系統(tǒng),αji即為α12或α21,且α12 = α21。Renon等根據(jù)相似化學(xué)理論,通過(guò)整理大量二元系統(tǒng)實(shí)驗(yàn)數(shù)據(jù)后發(fā)現(xiàn)α12變化約從0.20至0.47,并可根據(jù)溶液的不同類型設(shè)置不同的α12值。當(dāng)實(shí)驗(yàn)數(shù)據(jù)缺乏時(shí),α12的值常可任意規(guī)定,典型的選擇是α12=0.3。另外,在NRTL模型中,能量參數(shù)也可表達(dá)成為溫度的函數(shù),此取決于所研究體系的復(fù)雜性。
